
|
Einführung in die Erkenntnistheorie [Eine Auseinandersetzung mit dem Positivismus und dem erkenntnistheoretischen Idealismus] [ 4 / 4 ]
II. TEIL Systematische Entwicklung 1. Abschnitt Das Denken und die Logik vom erkenntnistheoretischen Standpunkt aus. (1) 1. Kapitel Welches Denken ist allgemeingültig? Der Denkende hält eine Betrachtungsweise, die ihm selbst als logisch zwingend erscheint, für allgemeingültig: für zwingend für ihn selbst zu jeder Zeit und für zwingend für alle Denkenden. Nicht als ob der Gedanke der Allgemeingültigkeit sich mit allen logisch zwingenden Betrachtungsweisen auch wirklich verbinden würde, aber, wo logisch zwingend gedacht wird, wird der Denkende auf die Frage nach der Allgemeingültigkeit des Gedachten diese behaupten. Wir wollen zunächst die Bestimmungen, die wir als allgemeingültig bezeichnen, noch näher charakterisieren. Wir sagten zunächst, die logischen zwingenden Denkakte werden als allgemeingültig angesprochen. Unser Denken vollzieht sich in Urteilen. Wir sprechen von Urteilen im psychologischen Sinn und im logischen Sinn. Für uns kommt es hier auf die Urteile in einem logischen Sinn an, aber eine Angabe darüber, was unter Urteilen in einem psychologischen Sinn zu verstehen ist, dürfte pädagogisch zweckmäßig sein, dadurch wird das Verständnis der Bestimmung über Urteile im logischen Sinn erleichtert. Es hat die Auffassung immer mehr Anklang gefunden, daß wir das Urteil im psychologischen Sinn als einen psychischen Vorgang anzusehen haben, der sich mit dem Bewußtsein der Gültigkeit verbindet. Diese Auffassung empfiehlt sich dadurch, daß es uns im Denken auf gültige Bestimmungen ankommt, und wir als Urteile diejenigen elementaren Akte bezeichnen wollen, welche als gültig aufgestellten Bestimmungen zugrunde liegen. Dieser Auffassung ist widersprochen worden, indem man sagte, daß sich bei wissenschaftlichem Denken durchaus nicht bei jedem Schritt das Bewußtsein der Gültigkeit nachweisen läßt. Wenn wir ein Buch lesen, tritt da bei jedem einzelnen Denkakt das Bewußtsein der Gültigkeit auf? Man sagt, daß dieses Bewußtsein sicherlich nicht bei jedem einzelnen Schritt im Denken zu konstatieren ist. Ist das aber nicht der Fall, so ist es nicht angängig, das Urteil als denjenigen Akt zu definieren, der sich mit dem Bewußtsein der Gültigkeit verbindet: man will ja doch mit dieser Definition die einzelnen Schritte treffen, die im Denken vollzogen werden. Diesen Streit glaube ich durch eine experimentelle Untersuchung über das Bewußtsein der Gültigkeit geschlichtet zu haben. Ich habe einfache Schlußprozesse daraufhin untersucht, wie es in den einzelnen Schritten des Denkens mit dem Bewußtsein der Gültigkeit steht (2). Dabei hat sich ergeben, daß tatsächlich nicht bei jedemm Schritt im Denken ein Bewußtsein der Gültigkeit auftritt. So zeigt sich, daß die Auffassung der einzelnen Prämissen eines Schlusses sich meist nicht mit dem Bewußtsein der Gültigkeit verbindet. Hier bei der Untersuchung von Schlüssen kann man nicht wie bei der Untersuchung isolierter Urteile sagen: nun, wenn kein Bewußtsein der Gültigkeit da war, dann war es eben kein Urteil. Aufgefaßten Prämissen, aus denen ein Schlußsatz mit dem Bewußtsein absoluter Gültigkeit gezogen ist, kann man natürlich nicht den Urteilscharakter absprechen. Deshalb ist die Untersuchung der Urteile in einfachen Schlüssen der Untersuchung isolierter Urteile vorzuziehen. Wenn aber auch die Auffassung einzelner Prämissen eines Schlusses sich meist nicht mit dem Bewußtsein der Gültigkeit verbunden zeigte, so war doch bei den einzelnen Schritten im Denken ein Äquivalent für dieses Bewußtsein der Gültigkeit nachzuweisen. Dieses Äquivalent stellte sich in den verschiedenen Fällen verschieden dar, überall war mit den einzelnen Schritten im Denken ein Etwas gegeben, so beschaffen, daß auf die Frage nach der Gültigkeit des betreffenden Schrittes eine Bejahung eingetreten ist.
Diese Bestimmung konnte aber nur als richtig anerkannt werden, indem man einseitig auf den Gegensatz der Logik zur Aufgabe der Psychologie achtete, eine Beschreibung des Urteilsprozesses zu geben. Hat denn die Naturwissenschaft es nicht auch mit dem Sinn der Urteile zu tun? Doch ohne Zweifel, auch sie hat es mit dem Sinn, mit den Gegenständen richtiger Urteile zu tun. Hier muß also jedenfalls eine ergänzende Bestimmung gemacht werden. Achten wir darauf, daß die Naturwissenschaft die Gegenstände der Urteile als Größen behandeln, die sind, auch wenn sich nicht gedacht werden. Die Logik dagegen betrachtet die Beziehungen der Gegenstände richtigen Urteilens untereinander im Denkgeschehen, wir können also sagen: die Logik hat es mit den Gegenständen richtiger Urteile als gedachten zu tun. Unter richtigem Denken verstehen wir aber psychische Vorgänge, die sich mit dem Bewußtsein absoluter, nicht mehr steigerungsfähiger Sicherheit verbinden oder die, ohne mit dem Bewußtsein dieser Sicherheit verbunden zu sein, so beschaffen sind, daß auf die Fragestellung nach der Richtigkeit eine Bejahung mit dem Bewußtsein absoluter, nicht mehr steigerungsfähiger Sicherheit erfolgt, und zwar durch die Zerlegung komplexer Operationen in elementare bei jedem Schritt. Jede elementare Operation dieses Denkens ist dann ein richtiges Urteil. Ich hebe sogleich hervor, daß dabei die Verifikationen nicht zu kurz kommen. Diese Feststellung möchte ich verteidigen gegenüber der Erfahrung der Täuschungen auf dem Gebiet der Denkoperationen. Es ist eine bekannte Tatsache, daß manche Behauptungen sich mit dem Bewußtsein der Gültigkeit oder Sicherheit verbinden, die sich bei weiterer Prüfung als falsch herausstellen. Diesen Tatbestand muß man im Auge behalten, um nicht das Auftreten des Bewußtseins der Denknotwendigkeit, der Gültigkeit von Gedachtem in seiner Bedeutung zu überschätzen. Andererseits darf man sich durch diesen Tatbestand nicht verführen lassen, wie das manche Autoren tun, nur dasjenige als allgemeingültig gelten zu lassen, was sich gehörig verifiziert hat. Wie steht es mit der Verifikation von Behauptungen? Betrifft eine Behauptung einzelne Tatbestände, so vollzieht sich die Verifikation durch einen Vergleich der Wirklichkeit mit der Behauptung. Es stellt dann ein Identitätsurteil die Übereinstimmung oder ein Differenzurteil die Nichtübereinstimmung einer Behauptung mit der Wirklichkeit fest. In der Wissenschaft betrifft die Verifikation meist die Behauptung abstrakter Beziehungen, so daß eine unmittelbare Vergleichung mit der Wirklichkeit nicht möglich ist. Die Verifikation wird dann so vollzogen, daß diese Behauptung als Prämisse in Schlußprozesse eingeht, aus denen sich dann eine Behauptung ergibt, die auf einzelne Tatbestände geht. Es wird dann also eine Verifikation durch Schlußprozesse und Identitätssetzung oder Differenzsetzung vollzogen. Bei diesen Verifikationen werden, wie man sieht, im einen Fall Identitäts- und Differenzsetzungen, in der anderen Klasse von Fällen Schlußprozesse und Identitäts- oder Differenzsetzungen als allgemeingültig vorausgesetzt - und zwar ohne daß man sich das gewöhnlich zu Bewußtsein bringt. Wollte man für die in den Schlußprozessen und in den Identitäts- und Differenzsetzungen gegebenen Denkprozess wieder Verifikationen verlangen, so würde man die Verifikation in infinitum fortsetzen müssen! Man kommt also nicht aus, ohne die Inanspruchnahme gewisser psychischer Akte als allgemeingültig ohne Verifikation. Was ich hier über die Verifikationstheorien gesagt habe, gilt natürlich auch für den Pragmatismus. Der Pragmatismus hält diejenigen Vorstellungsweisen für allgemeingültig, welche sich in unserem Handeln bewähren, welche in unserem Handeln unsere Lebensinteressen fördern. Er stellt also eine bestimmte Art von Verifikationstheorie dar. Welche psychischen Akte sind nun aber als allgemeingültig ohne Verifikation anzusetzen? Jedenfalls nicht alle Akte, die sich mit dem Bewußtsein der Gültigkeit, der Sicherheit verbinden. Welche denn? Nimmt man eine nähere Untersuchung des Bewußtseins der Gültigkeit von Gedachtem vor, so findet man, daß der Charakter der Gültigkeit oder Sicherheit von sehr differenter Art ist. (3) Mit dem Vollzug von psychischen Akten kann sich ein Charakter der Sicherheit verbinden, so wenig ausgeprägt, daß auf die Fragestellung nach der Richtigkeit eine Bejahung nicht mit absoluter Sicherheit erfolgt, aber mit einer Sicherheit, wie sie für unsere praktischen Zwecke meist genügt. Mit dem Vollzug von psychischen Akten kann sich aber auch ein Charakter der Sicherheit solcher Art verbinden, daß auf die Frage nach der Richtigkeit eine Bejahung mit dem Bewußtsein absoluter, nicht mehr steigerungsfähiger Sicherheit erfolgt (4). Diese absolute, nicht mehr steigerungsfähige Sicherheit hebt sich deutlich von der Sicherheit ab, mit der man ich meist im gewöhnlichen Leben und sogar im wissenschaftlichen Denken meist begnügt. Eine nähere Beschreibung dieser Differenzen der Sicherheit gehört in die Psychologie, die Aufweisung der Differenz zwischen absoluter, nicht mehr steigerungsfähiger Sicherheit und den verschiedenen niederen Graden der Sicherheit ist aber Sache der Logik und Erkenntnistheorie. Ist der Zustand der Sicherheit wenig ausgeprägt, so ist eine Verwechslung mit einem assoziativ bedingten Zwangsgefühl möglich. Das führt zu manchen Irrtümern im Denken. Nachdem wir erkannt haben, daß wir jedenfalls irgendwelche psychischen Akte als allgemeingültig ohne Verifikationen ansetzen müssen, werden wir auf die Frage, welche psychischen Vorgänge wir denn nun als allgemeingültig ohne Verifikation bezeichnen werden, antworten: psychische Vorgänge, mit denen sich ein Bewußtsein absoluter, nicht mehr steigerungsfähiger Sicherheit verbindet oder mit denen der Zustand absoluter, nicht mehr steigerungsfähiger Sicherheit gegeben ist, d. h. bei denen, ohn daß dieses Bewußtsein der Sicherheit vorhanden ist, auf Fragestellung eine Bejahung mit dieser Sicherheit erfolgt, und zwar bei der Zerlegung in elementare Operationen. Andere Irrtümer im Denken entspringen daraus, daß einem Sicherheitsbewußtsein eine falsche Beziehung gegeben wird, so bei Wahrnehmungsurteilen eine Beziehung auf die Objekte anstatt auf die Wahrnehmungsinhalte, oder bei einem Schlußprozeß, in welchem bei der Entwicklung des Schlußsatzes aus einem synthetisch aus den Prämissen gewonnenen Gesamttatbestand ein Sicherheitsbewußtsein auftrat, in früheren Schritten aber nicht, eine Beziehung auf die ganzen Schlußoperationen anstatt auf den letzten Schritt. Die Richtigkeit des Ergebnisses, das wir gewonnen haben, wird uns am leichtesten der formale Logiker und der Mathematiker bestätigen können, oder sagen wir lieber der Logiker und der Arithmetiker. Denn wenn der Logiker Bestimmungen macht wie die:
Wenn C ist, so ist D Also wenn A ist, so ist D, oder Wenn K ist, so ist F, Nun ist F nicht, Also ist K nicht. Der Naturwissenschaftler wird aber geneigt sein zu sagen, daß bei ihm Bestimmungen, die mit absoluter, nicht mehr steigerungsfähiger Sicherheit gelten, sehr selten sind. Er sagt uns: ich arbeit meist mit Verifikationen und diese führen mich zu Wahrscheinlichkeitsurteilen. Die Gewißheit also, mit der ich es zu tun habe, muß geschieden werden von der oben bezeichneten Art der Gewißheit. Darauf ist zu antworten: In den Wahrscheinlichkeitsurteilen wird nur eine mehr oder weniger große Wahrscheinlichkeit behauptet, aber diese Behauptung wird gemacht, wenn es eine wissenschaftlich gültige Behauptung ist, mit absoluter, nicht mehr steigerungsfähiger Sicherheit. Es gilt also auch für die durch Verifikation gewonnenen Behauptungen, daß sie den Charakter absoluter, nicht mehr steigerungsfähiger Sicherheit tragen. Und wenn aufgrund einer Verifikation eine Annahme mit der und der Wahrscheinlichkeit gilt, so kann eben nur unter Benutzung der Verifikation mit absoluter nicht mehr steigerungsfähiger Sicherheit behauptet werden, daß die Annahme mit der und der Wahrscheinlichkeit gilt. Man wird uns vielleicht noch einwenden, wir verwischen den Unterschied zwischen tatsächlichen Wahrheiten und notwendigen Wahrheiten. Der Logiker und Arithmetiker haben es mit denknotwendigen Wahrheiten zu tun, der Naturwissenschaftler mit tatsächlichen. Nehmen wir Beispiele. Der Naturwissenschaftler stellt die Behauptung auf: Angelassener Gußstahl hat bei 10° C den Elastizitätskoeffizienten 19014. Das ist nun eine tatsächliche Wahrheit. Wenn aber der Arithmetiker sagt: 7 + 5 = 12, so ist dies eine notwendige Wahrheit. Ich kann mir nicht denken, daß 7 + 5 nicht gleich 12 ist, also das kontradiktorische Gegenteil dieser Bestimmung kann ich nicht ohne Widerspruch denken. Ich kann mir aber sehr wohl denken, ohne einen Widerspruch im Denken zu begehen, daß Gußstahl einen anderen Elastizitätskoeffizienten hat. Sehen wir uns diese verschiedenen Arten von Bestimmungen näher an, so wird sich zeigen, daß unsere obige Behauptung sich mit der Aufrechterhaltung dieser Unterschiede verträgt. In der Feststellung, daß Gußstahl bei der und der Temperatur den und die Elastizitätskoeffizienten hat, ist eine Beziehung zwischen Gußstahl und dem Elastizitätskoeffizienten behauptet, die ich nicht durch bloßes Denken gewinnen kann, die nicht denknotwendig ist. Denknotwendig ist aber die Setzung dieser Beziehung an der Hand des gegebenen Tatbestandes (bei Voraussetzung der Gültigkeit der Deutung der Wahrnehmungsinhalte). Allgemein können wir also sagen: Bei Tatsachenwahrheiten ist denknotwendig die Beziehung zwischen dem unter einem bestimmten Gesichtspunkt betrachteten, unmittelbar gegebenen Tatbestand und der Behauptung einer bestimmten Beziehung, aber nicht die behaupteten Beziehungen. In der Feststellung: 7 + 5 = 12 ist eine Beziehung zwischen 7 + 5 und 12 behauptet, die ich nicht in der Erfahrung vorfinde, sondern durch Denken erzeuge. Allgemein können wir also sagen: Bei notwendigen Wahrheiten sind die in diesen Sätzen behaupteten Beziehungen nicht in der Erfahrung vorgefunden, sondern durch das Denken selbst erzeugt. Man kann also den Unterschied zwischen tatsächlichen Wahrheiten und notwendigen Wahrheiten betonen und dabei behaupten, daß wir es in beiden mit denknotwendigen Bestimmungen zu tun haben oder, wie wir sagen, mit Bestimmungen, welche den Charakter absoluter, nicht mehr steigerungsfähiger Sicherheit haben. Es bleibt also bei unserer Bestimmung, daß diejenigen Bestimmungen in den Wissenschaften als allgemeingültig angesetzt werden, die bei der Zerlegung in elementare Operationen mit absoluter, nicht mehr steigerungsfähiger Sicherheit vollzogen werden. Die Frage der Möglichkeit der Rechtfertigung der Ansetzung von Bestimmungen als allgemeingültig. Es fragt sich nun, wie es mit der Möglichkeit der Rechtfertigung der Ansetzung von Bestimmungen als allgemeingültig steht. Eine solche Rechtfertigung ist kürzlich in einer interessanten Weise von RICKERT zu geben versucht worden. Nach RICKERT handelt es sich in den Urteilen um die Anerkennung eines Wertes, eines Sollens. Ich erwähne das hier nur der Terminologie wegen, bei kritischer Behandlung anderweitiger Vorstellungsweisen von RICKERT werde ich kritisch diese Vorstellung näher ins Auge fassen. Also es handelt sich im Urteil um die Anerkennung eines Sollens.
Kann man an der transzendenten Gültigkeit des Sollens, mit dem wir es beim Urteil zu tun haben, zweifeln? RICKERT antwortet: das ist nicht angängig, weil zweifeln heißt: ist dieses Urteil wahr oder das entgegengesetzte? muß ich Ja oder Nein sagen? Die Frage setzt voraus: nur eines von beiden Urteilen (das hier vollzogene oder das kontradiktorisch entgegengesetzte) kann wahr sein, aber eines muß wahr sein. Man kann immer nur zweifeln, ob so oder so geurteilt wird, aber nicht, ob überhaupt. Also führt es zum Widerspruch, an der transzendenten Gültigkeit des Sollens zu zweifeln, das Zweifeln involviert eben die Anerkennung eines transzendenten Sollens (7). Also der Zweifel soll die Anerkennung des Sollens als eines transzendenten einschließen. Aber wenn man zugibt, daß mit dem Zweifeln die Behauptung gesetzt ist: Dieses Urteil ist entweder wahr oder falsch, so würde das Zweifeln an den einzelnen Urteilen zum höchsten zu der Anerkennung des Satzes führen, daß man einer Behauptung gegenüber sich entweder bejahend oder verneinend verhalten muß. Damit ist aber noch wenig gewonnen. Es kommt darauf an, das Sollen überhaupt als ein solches von transzendenter Gültigkeit zu charakterisieren. Hier wäre aber zum höchsten das Sollen in Bezug auf ein Urteil als transzendent gültig implizit zuzugeben; es wäre damit nur der Satz als allgemeingültig anerkannt, daß eine Behauptung entweder wahr oder falsch ist, nicht aber wäre irgendein anderes Sollen damit als transzendent gültig implizit zuzugeben! Es soll aber jedes Sollen damit als transzendent gültig charakterisiert sein. Werden wir denn nun auf eine Rechtfertigung der Ansetzung gewisser Bestimmungen als allgemeingültig verzichten müssen? Wollte jemand den Anspruch erheben, die Allgemeingültigkeit gewisser Arten von Bestimmungen zu beweisen - im gewöhnlichen Sinn des Wortes - so würde dieser Beweis den Anspruch auf Allgemeingültigkeit erheben, und dieser Anspruch würde sich doch wohl wieder auf eine bestimmte Art von Sicherheit in letzter Linie stützen, mit der die einzelnen Schritte dieses Beweises vollzogen werden; es würde also das zu Beweisende vorausgesetzt sein. Vielleicht können wir aber sagen, daß der Anspruch gewisser psychischer Akte auf Allgemeingültigkeit sich in einemfort bestätigt? Das ist nicht richtig, wenn man die Bestätigung im Sinne einer allgemeingültigen Feststellung faßt, aber es ist allerdings richtig, wenn man damit eine Bestätigung im Denken des einzelnen Denkenden meint: ich kann ja doch Denkakte vollziehen in der Weise, daß ich sage: mir stellt sich diese Betrachtungweise als eine von absoluter, nicht mehr steigerungsfähiger Sicherheit dar und im speziellen hier: mir stellen sich diese Bestätigungen als solche von absoluter, nicht mehr steigerungsfähiger Sicherheit dar. Hier ist natürlich noch nicht von der Gültigkeit des Denkens für etwaige unabhängig von ihm seiend gedachte Objekte die Rede, davon handeln wir erst später. Die Allgemeingültigkeit und der Satz vom unmittelbaren Bewußtsein. Modifizierung desselben. Ich möchte nun weiter die Allgemeingültigkeit gewisser Denkakte zum sogenannten Satz vom unmittelbaren Bewußtsein in Beziehung setzen. Man versteht unter dem Satz vom unmittelbaren Bewußtsein gewöhnlich die Behauptung, daß die Bewußtseinsvorgänge, die einem einzelnen Subjekt in einem bestimmten Moment vorhanden zu sein scheinen, auch wirklich vorhanden sind. Ich halte es für nötig, diese Bestimmung einzuschränken. - Werfen wir aber zunächst einen Blick auf die Hauptetappen der Entwicklung der Lehre vom unmittelbaren Bewußtsein. Diesen Satz hat, wie es scheint, PROTAGORAS zuerst aufgestellt und zwar in der Form:
Die Behauptung von CARTESIUS schließt allerdings mehr als als das von uns oben Bezeichnete. Für ihn ist auch das Vorhandensein einer Ich-Substanz eine unbezweifelbare Tatsache.
Zuletzt erwähne ich nur noch die Ausprägung dieses Prinzips bei HERBART. HERBART sagt, was mit unserem Prinzip gemeint ist, tritt besonders deutlich hervor, wenn wir es auf Fälle illusionärer Wahrnehmung anwenden. Da haben wir es mit einem Schein zu tun, aber dieser Schein ist doch, das Sein dieser illusionären Wahrnehmung ist jedenfalls eine unbezweifelbare Tatsache.
Man könnte geneigt sein zu denken, daß eine Täuschung in Bezug auf unsere unmittelbar gegebenen Bewußtseinsvorgänge nicht möglich ist. Man könnte da etwa Folgendes sagen: Eine wesentliche Quelle der Wahrnehmungsillusion ist darin gegeben, daß gewisse Empfindungen unter bestimmten Bedingungen Vorstellungen reproduzieren und mit ihnen verschmelzen, welche dem vorhandenen Reiz nicht entsprechen. Eine Jllusion bezüglich der unmittelbar gegebenen Bewußtseinsvorgänge müßte man sich dann, so könnte man sagen, so denken, daß ein Bewußtseinsvorgang unter bestimmten Bedingungen einen psychischen Vorgang reproduziert und mit ihm verschmilzt, der inhaltlich von ihm verschieden ist. Dies ist der einzige Weg, würde man sagen, der in Frage kommt zur Erzeugung einer Jllusion in Bezug auf die unmittelbar gegebenen Bewußtseinsvorgänge. Tatsächlich aber wird auf diesem Weg keine Jllusion erzeugt, denn wenn reproduzierte psychische Vorgänge mit vorhandenen Vorgängen verschmelzen, so wird dadurch der ursprüngliche Vorgang tatsächlich zu einem anderen. Hier, wie die Aussage das im Bewußtsein Gegebene betrifft, können Assimilationsprozesse nicht zu Täuschungen Anlaß geben. Dagegen ist aber geltend zu machen, daß ich mich in der näheren begrifflichen Charakterisierung meiner Bewußtseinsvorgänge täuschen kann. Jene Charakterisierung findet durch Vorstellungen statt, die nicht mit dem gegebenen psychischen Tatbestand verschmelzen. Jeder wird mir z. B. zugeben, daß ich bei einer Empfindung geringer Intensität darüber in Zweifel sein kann, ob damit etwas, was wir Gefühl nennen, gegeben war oder nicht. Ich kann sodann in einem auf den betreffenden psychischen Vorgang unmittelbar folgenden Zeitmoment in das Erlebnis aufgrund eines vorhandenen Vorurteils etwas hineinsehen, was nicht darin gelegen ist. Das ist der gewöhnlichste Fehler der Selbstbeobachtung bei einem Individuum, welches mit mehr oder weniger fertigen Theorien im Kopf an das Beschreiben von Erlebnissen herantritt. Durch diese Feststellung scheint nun die Gültigkeit der Aussagen über das, was wir erleben, ganz ins Wanken zu kommen. Allen irgendwie beschaffenen Zweifeln am Satz vom unmittelbaren Bewußtsein könnte man begegnen, wenn es gelänge, zu zeigen, daß derselbe oder wenigstens eine Einschränkung desselben eine notwendige Voraussetzung allen Erkennens darstellt! Das ist aber der Fall. Bedingung für alles Erkennen ist, daß das mit absoluter, nicht mehr steigerungsfähiger Sicherheit als gedacht Erscheinende auch wirklich gedacht ist. Wir setzen deshalb die in Erlebnissen mit dem Charakter absoluter, nicht mehr steigerungsfähiger Sicherheit als gedacht erscheinenden Gegenstände als wirklich gedacht und zwar mit diesem Charakter der Sicherheit. Damit ist, wie man sieht, eine Einschränkung des Satzes vom unmittelbaren Bewußtsein vollzogen, man würde ihn bei dieser Einschränkung am besten bezeichnen als den "Satz von der Wirklichkeit des in Erlebnissen mit dem Charakter absoluter, nicht mehr steigerungsfähiger Sicherheit als gedacht Erscheinenden". In welcher Beziehung steht nun dieser Satz zur Annahme der Allgemeingültigkeit gewisser Denkprozesse? Die Allgemeingültigkeit gewisser Denkprozesse ist mit diesem Satz noch nicht gesetzt: das in Denkprozessen Gemeinte kann wirklich gemeint sein, ohne daß es richtig gemeint ist. Aber die Setzung dieses Satzes als gültig ist eingeschlossen, wenn auch nicht ausgesprochen in der Annahme der Allgemeingültigkeit gewisser Erlebnisse. Die soeben vollzogene Einschränkung des Satzes vom unmittelbaren Bewußtsein wird sich uns von großer Bedeutung für unsere weiteren erkenntnistheoretischen Entwicklungen zeigen. So werden wir nicht, wie der Positivist, jede Empfindung als (erkenntnistheoretisch) gegeben betrachten können, sondern nur diejenigen sind uns erkenntnistheoretisch gegeben, welche Gegenstände so und so beschaffener Denkprozesse sind. Leistungsfähigkeit des Denkens. Synthetische Urteile a priori. Kritischer Rationalismus bezüglich der formalen Wissenschaften ohne psychologischen Apriorismus. Nachdem ich die Allgemeingültigkeit [storring] des Denkens und den sogenannten Satz vom unmittelbaren Bewußtsein behandelt habe, will ich die Leistungsfähigkeit des Denkens näher untersuchen. Ich will sie zunächst gegen Einwände der Skeptiker verteidigen und dann positive Entwicklungen darüber geben. a) Wenn die alten Skeptiker gegen die Möglichkeit des Syllogismus einwandten, die Prämissen eines Syllogismus müßten doch selbst wieder bewiesen werden und so ad infinitum, so ist dagegen einmal einzuwenden, daß dieser Einwand nicht für einen Schluß wie den gelten kann:
und alle B zur Gattung C gehören, so gehören alle (einige A) zur Gattung C. Bekannter ist der Einwand der Skeptiker, daß der Obersatz im Syllogismus den Schlußsatz schon voraussetzt, so daß jeder Schluß eine petition principii [es wird vorausgesetzt, was erst zu beweisen wäre - wp] darstellt. In Anerkennung dieses Einwandes hörten wir JOHN STUART MILL entwickeln, daß der eigentliche Schluß nicht hier bei Übergang vom Allgemeinen zum Einzelnen liegt, sondern man schließt von beobachteten Einzelfällen auf nicht beobachtete Einzelfälle oder auch auf alle Fälle einer bestimmten Klasse. Gegen diese Entwicklungen MILLs haben wir einzuwenden: wir sind nicht sicher, daß gerade CAJUS auch sterblich ist, wenn wir nicht wissen, daß alle Menschen sterblich sind. Nur wenn wir wissen, daß alle Menschen sterblich sind, ist uns eine logische Garantie gegeben, daß auch CAJUS sterblich ist. Es mag sein, daß sich psychologisch konstatieren läßt, daß manche Menschen in der von MILL charakterisierten Weise schließen, es fragt sich aber dann immer noch, ob das mit Recht geschieht. Wir würden sagen, wenn manche Menschen so schließen, so ist das kein psychischer Vorgang, der sich mit absoluter, nicht mehr steigerungsfähiger Sicherheit vollzieht. Die ganze Schwierigkeit bezüglich der vermeintlichen petitio principii wird gehoben, wenn wir folgende Distinktion machen: in dem Gesamtbestand, der gemeint ist, wenn wir sagen, daß alle Menschen sterblich sind, liegt ohne Zweifel die einzelne Tatsache, bezeichnet durch die Behauptung "Cajus ist sterblich" eingeschlossen. Aber in unserem Denken kommen wir auf die Feststellung "alle Menschen sind sterblich", ohne das Urteil zu fällen "Cajus ist sterblich". Die Tatsache, die uns gegeben ist im Tod der früheren Generationen der Menschen, bringt uns zusammen mit der Annahme der Gültigkeit des allgemeinen Kausalprinzips auf die Feststellung der Gültigkeit des Satzes "alle Menschen sind sterblich". Es handelt sich hier also im Grund um eine Verwechslung von Denken und Sein. (13) b) Wir wollen jetzt dazu übergehen, die positive Enwicklung der Leistungsfähigkeit des Denkens zu geben. Daß durch die Denkprozesse in Schlüssen neue Wahrheiten gewonnen werden, ist am deutlichsten aus solchen Schlüssen zu ersehen, deren Prämissen räumliche, zeitliche Beziehungen oder die Beziehungen größter und kleiner haben. Nehmen wir den Schluß:
k ist größer als f also ist p größer als f. Wir können den Tatbestand auch so ausdrücken: Der Schlußsatz stellt hier eine analytische Bestimmung dar in Relation zu dem durch eine Synthesis der Prämissen gewonnenen Gesamttatbestand (wobei wir analytisch eine Bestimmung in Relation zu einem anderen nennen, wenn sie aus dieser anderen gewonnen werden kann, ohne daß man über das in dieser anderen Behauptung Gegebene hinausgeht). Den einzelnen Prämissen gegenüber ist dagegen der Schlußsatz keine analytisch gewonnene Bestimmung, es ist also eine synthetische Behauptung in Relation zu den einzelnen Prämissen. Die Leistungsfähigkeit des Denkens wird weiter noch in ein besonderes Licht gerückt, wenn man auf folgende Tatbestände hinweist. Nehmen wir einen einfachen Schluß: Wenn eine erstgedachte Größe (v) kleiner als eine zweitgedachte (d) ist und eine drittgedachte Größe (k) kleiner als die erstgedachte (v), so ist die drittgedachte Größe (k) kleiner als die zweitgedachte (d). Das ist eine Bestimmung, welche für unendlich viele Fälle gilt. Wenn ein erstgedachter Körper links von einem zweitgedachten liegt und ein drittgedachter rechts von dem zu zweitgedachten, so liegt der zuerst gedachte links von dem zu drittgedachten. Das ist ebenfalls eine Bestimmung, die für unendlich viele Fälle gilt. Ebenso steht es bei dem Schluß: Wenn eine erstgedachte Gruppe von Körpern zu einer zu zweit gedachten Gattung gehört und diese Gattung zu einer zu dritt gedachten Gattung, so gehört die erstgedachte Gruppe von Körpern zu der zu dritt gedachten Gattung. Wie steht es mit diesen Bestimmungen, welche für unendlich viele Fälle gelten? Stützen sich dieselben vielleicht auf einzelne Beobachtungen? Sage ich:
Ich habe vielleicht häufig die Erfahrung gemacht, daß ein bestimmter Vorgang, den wir a nennen wollen, später als ein bestimmter Vorgang aufgetreten ist, den wir b nennen wollen, und daß ein Vorgang c früher war als der Vorgang b. Da haben wir festgestellt, daß a später als c war. Aber wie kann ich mit logischem Recht von einzelnen Fällen auf unendlich viele Fälle schließen? - und ich muß doch den Anspruch erheben, daß meine Bestimmung für unendlich viele Fälle gilt! Oder sind vielleicht jene allgemeinen Sätze, die für unendlich viele Fälle gelten, angeboren, so daß einem Schluß wie
Vorgang c früher als Vorgang b Also Vorgang a später als Vorgang c. Wenn ein erstgedachter Vorgang später als ein zweitgedachter ist und ein drittgedachter früher als ein zweitgedachter, so ist auch der erstgedachte später als der drittgedachte. Nun ist aber der Vorgang a später als der Vorgang b etc.: Also ist auch der Vorgang a später als c. Diese allgemeinen Sätze als angeboren aufzufassen, wird wohl keinem im Ernst einfallen, sonst müßte auch ein Satz angeboren sein, wie dieser:
Wählen wir zunächst einen räumlichen Schluß. Es wird sich uns zeigen, daß bei Schlüssen mit zeitlichen Beziehungen, bei Schlüssen mit den Beziehungen größer - kleiner und auch bei einer Klasse von Subsumtionsschlüssen dieselben Verhältnisse vorliegen. Habe ich die Prämissen:
"Ein erstgedachter Körper (c) ist rechts von einem zweitgedachten (k)". Diese Bestimmung veranlaßt auch, das c an eine bestimmte Stelle rechts von k zu setzen (Figur 1) - 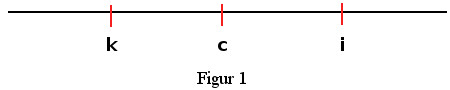 mit welchem Recht? es liegen da doch unendlich viele Möglichkeiten für die Lokalisierung von c vor. Die Setzung von c an eine bestimmte Stelle hat nur repräsentative Bedeutung. Diese bestimmte Stelle hat nur repräsentative Bedeutung. Diese bestimmte Stelle in Relation zur Stelle von k dient nur als Repräsentant für die gedachte Lage von c und zwar dient sie als Repräsentant, weil sie mit unendlich vielen Fällen, die bezeichnet sind durch die Bestimmung c rechts von k das gemeinsam hat, daß eine Bewegung nach ein und derselben Richtung dazu gehört, um von k nach dieser bestimmten Stelle und von k zu den unendlich vielen Stellen zu gelangen, welche durch die Bestimmung c rechts von k bezeichnet sind. "Ein drittgedachter Körper (i) ist rechts vom erstgedachten Körper (c)" [d. h. in derselben Richtung]. Der Punkt c mag liegen von c, in welcher Entfernung er will, ich kann darüber immer noch weiter nach rechts hinausgehen. Die bestimmte repräsentative Lokalisation erfolgt mit gleichem Recht wie vorher für c. Was hat nun die Bestimmung für unendlich viele Fälle ermöglicht? Der Umstand, daß sich unendlich viele Fälle durch einen Fall repräsentieren lassen, mit einem Fall in der für diesen Schluß ausschlaggebenden Beziehungen übereinstimmen. Diese Gleichheit der Beziehungen in unendlich vielen Fällen stellt aber eine Eigentümlichkeit der räumlichen Beziehungen dar. Diese Verwertung der Gleichheit der Beziehungen in unendlich vielen Fällen hat aber wieder zur Voraussetzung, daß sich uns die räumlichen Beziehungen isoliert darstellen. Daß sich uns aber die räumlichen Beziehungen isoliert darstellen, haben wir unserer Fähigkeit zur Abstraktion zu verdanken. Ähnlich wie bei Schlüssen mit räumlichen Beziehungen steht es bei Schlüssen mit zeitlichen Beziehungen. Die Beziehungen in der Zahlenreihe, mit denen wir es etwa zu tun haben bei dem Schluß:
Dieselbe Betrachtungsweise läßt sich auf Prämissen mit Gattungsbeziehungen anwenden. Denn die Gattungsbeziehungen lassen sich, wenn man mit Hilfe der Umfangsbeziehungen schließt, durch Raumstrecken, Zeitstrecken oder Strecken in der Zahlreihe repräsentieren. Haben wir es mit Prämissen zu tun: Eine erstgedachte Gattung (A) gehört zu einer zweitgedachten (höheren) Gattung (B) und diese zweitgedachte Gattung (B) zu einer drittgedachten (C), so läßt sich (Figur 2)  der Umfang der erstgedachten Gattung A durch die Strecke a b repräsentieren, die zweitgedachte Gattung B durch die Strecke a c, die drittgedachte Gattung C durch die Strecke a d. Es ergibt sich aus dem so gewonnenen repräsentativen Gesamttatbestand auf dieselbe Weise, wie bei den Schlüssen mit räumlichen (15), zeitlichen (16) Beziehungen und den Beziehungen "größer-kleiner" (17) unter Anlegung des durch die Einstellung zum Schluß gegebenen Gesichtspunktes (der darin besteht, die in den Prämissen noch nicht in Beziehung gesetzten Größen der Prämissen zueinander in Beziehung zu setzen), daß die Gattung A zu Gattung C gehört (18). Die Ansetzung des a c als Repräsentation für Gattung B in Relation zu a b und die Ansetzung des a d als Repräsentation für Gattung C ist ähnlich vermittelt, wie vorher. Auf einen Unterschied muß ich aber noch aufmerksam machen: im Falle der Schlüsse mit räumlichen Beziehungen, zeitlichen Beziehungen und den Beziehungen "größer-kleiner" gelten die allgemeinen Schlüsse für unendlich viele Fälle, wie wir sehen; daß es aber im Fall der Gattungsbeziehungen unendlich viele Fälle gibt, für welche diese Bestimmungen gelten, liegt nicht im Begriff der Gattungsbeziehung, aber wenn es unendlich viele Fälle gibt, dann gelten für sie die gemachten Bestimungen. Bei allen diesen allgemeinen Schlüssen mit den verschiedensten Beziehungen handelt es sich also um synthetische Bestimmungen, wie ich vorher nachgewiesen habe - und sodann um Bestimmungen für unendlich viele Fälle, wie ich soeben nachgewiesen habe. Da diese Bestimmungen über unendlich viele Fälle unabhängig von der Erfahrung erfolgen, so können wir sie auch apriorische Bestimmungen nennen. Wir haben es hier also mit synthetischen Bestimmungen a priori zu tun. Diese Feststellung ist natürlich von größter Bedeutung für die Lösung der kantischen Frage nach den synthetischen Urteilen a priori, zumal sich später zeigen wird, daß eine Bestimmung wie die 7 + 5 = 12 kein eigentliches Urteil ist, sondern ein Schluß; wir werden nämlich zwei große Klassen von Schlüssen zu unterscheiden haben: solche mit und ohne Mittelbegriffe. Ich habe nun noch andere Arten der Gewinnung des Schlußsatzes aus gegebenen Prämissen zu berücksichtigen und wir wollen sehen, ob dort ähnliche Verhältnisse vorliegen. Wenn ich die Prämissen habe:
So kann ich hier den Gedanken der Gleichheit der in den Prämissen gesetzten Beziehungen entwickeln und sagen: Wenn ein erstgedachter Vorgang (v) früher als ein zweitgedachter Vorgang (s) und ein drittgedachter Vorgang (k) früher ist, als der erstgedachte Vorgang (v); so ist also der drittgedachte Vorgang (k) noch früher, also erst recht früher als der zweitgedachte Vorgang (s). Oder anders ausgedrückt, ich kann schließen: was ich vom erstgedachten Vorgang (v) in Bezug auf den zweitgedachten Vorgang (s) aussagen kann, das kann ich von dem drittgedachten Vorgang (k) in Bezug auf den zweitgedachten Vorgang (s) wegen der Gleichheit der Beziehungen erst recht aussagen. Diese Schlußweise findet nicht nur bei den Schlüssen mit zeitlichen Beziehungen statt, sondern auch bei den Schlüssen mit räumlichen (19) Beziehungen und mit den Beziehungen größer - kleiner (20). Bei Schlüssen mit Gattungsbeziehungen ist hier die Analogie nur eine teilweise (21); wir werden die Schlußweise, welche die Analogie zu dieser bei Gattungsschlüssen darstellt, später kennen lernen. Allgemein läßt sich diese Schlußweise folgendermaßen charakterisieren: Es findet eine Gleichsetzung von Beziehungen statt, die entweder in den Prämissen schon unmittelbar gesetzt sind oder sich durch Konversion ergeben haben. Diese Gleichsetzung von Beziehungen wird nun so verwertet, daß man ausgeht von der Feststellung der Beziehung, die gegeben ist beim Übergang in einem Beziehungskomplex, von der als Mittelbegriff funktionierenden Größe zu einer der beiden anderen Größen. Von der zweitgedachten Größe wird dann gesagt, daß von ihr wegen der Gleichheit der Beziehungen auch oder erst recht gilt, was vom Mittelbegriff gilt. Oder diese Gleichsetzung von Beziehungen wird so verwertet, daß man von der Feststellung der Beziehung ausgeht, die gegeben ist beim Übergang in dem Beziehungskomplex zu der als Mittelbegriff funktionierenden Größe von einer der beiden anderen Größen aus. Von dieser letzteren Größe wird dann gesagt, daß die Beziehung, welche beim Übergang von ihr zum Mittelbegriff besteht, wegen jener Gleichheit der Beziehungen auch oder erst recht beim Übergang von ihr zu der zweiten anderen Größe vorliegt. Bei einer embryonalen Form dieser Operationsweise bestimmt die Auffassung der Gleichheit der Beziehungen nur die Synthesis der Beziehungsgedanken zu einem anschaulichen Gesamttatbestand, worauf dann ein Ablesen stattfindet. Diese embryonale Form ist dieser Operationsweise mit einer Operationsweise gemeinsam, in welcher der Gedanke der Gleichheit eine andere Verwertung findet, die ich nachher besprechen werde. Hier liegen die Verhältnisse in Bezug auf die Gewinnung einer Bestimmung für unendlich viele Fälle ganz ähnlich wie früher beim Schließen ohne Verwertung des Gedankens der Gleichheit oder des Gegensatzes der in den Prämissen gesetzten Beziehungen beim Schließen. In dem zuletzt erwähnten Beispiel, in welchem ein erstgedachter Vorgang (r) früher als ein zweitgedachter Vorgang (s) gesetzt war und ein drittgedachter Vorgang (k) früher als der erstgedachte Vorgang (r), kann sich auf die Bestimmung k noch früher der Schluß gründen, also erst recht früher als s, weil die unendlich vielen Fälle, die alle die Bedingung erfüllen, daß sie noch früher (als r) sind, in dem einen Punkt übereinstimmen, daß sie noch weiter als r von s aus nach derselben Richtung hin liegen. Also auch hier ist der Schluß, welcher für unendlich viele Fälle gilt, dadurch bedingt, daß unendlich viele Fälle in einem Punkt übereinstimmen, der für den Schluß verwertet wird; daß es unendlich viele solcher Fälle gibt, die in einem Punkt übereinstimmen, ist durch die Gleichförmigkeit der Raum-, Zeit und Zahlgebilde bedingt. - Der Gedanke der Gleichheit der in den Prämissen gesetzten Beziehungen kann sodann noch in einer anderen Weise zum Zustandekommen des Schlusses beitragen. Wenn ich die Prämisen habe:
Es handelt sich hier also darum, daß man bei Auffassung der Prämissen von der Größe i ausgehend zwei Übergänge vollzieht und bei dem zweiten Übergang (zu u) das Bewußtsein hat, beidemale in der gleichen Richtung, zu kleineren Größen weitergegangen zu sein; dieses Bewußtsein gleichen Fortschreitens wird nun so verwendet, daß man in Bezug auf die Größe, bei derm an stehen bleibt, hier u, sagt, daß sie am meisten nach derjenigen Richtung liegt, in der das Fortschreiten erfolgt ist, hier zu der kleineren Größe. Also ist u auch kleiner als diejenige Größe, welche den Anfangspunkt des Beziehungssetzens bildete, nämlich i. Diese Schlußweise findet sich nicht nur bei Prämissen mit den Beziehungen "größer - kleiner", sondern auch bei Prämissen mit räumlichen und zeitlichen Beziehungen und hier findet man auch wieder eine völlige Analogie bei Schlüssen mit einer Subsumtionsbeziehung. Habe ich die Prämissen:
Allgemein läßt sich diese Operationsweise folgendermaßen charakterisieren: Es findet eine Gleichsetzung von Beziehungen statt, die entweder in den Prämissen schon unmittelbar gesetzt sind oder sich durch Konversion ergeben haben. Beim Durchlaufen dieser Beziehungen kommt die Gleichheit derselben in dem Gedanken des Fortschreitens nach ein und derselben Richtung zu Bewußtsein. Dieser Gedanke der Gleichheit des Fortschreitens wird nun so verwertet, daß man von derjenigen Größe, welche das zuletzt gesetzte Beziehungsglied darstellt, aussagt, daß sie am weitesten nach dieser Richtung hin gelegen ist, also auch nach dieser Richtung von der Ausgangsgröße aus liegt. Die Gültigkeit dieser Art von Schlüssen für unendlich viele Fälle ergibt sich durch eine ähnliche Betrachtung wie bei der vorigen Operationsweise. Ich habe nun von der Verwertung des Gedankens des Gegensatzes der in den Prämissen gesetzten Beziehungen beim Schluß zu sprechen. Nehme ich die Prämissen: Ein erstgedachter Körper (J) liegt links von einem zweitgedachten (L). Ein drittgedachter Körper (M) liegt rechts vom zweitgedachten (L), so kann der Gedanke entwickelt werden:
Es wurde von den in den Prämissen aufeinander bezogenen Größen die nicht als Mittelbegriff funktionierenden als in entgegengesetzten Richtungen liegend aufgefaßt. Diese Setzung entgegengesetzter Richtungen wird nun so verwertet, daß man ausgeht von der Feststellung der Beziehung, die gegeben ist beim Übergang im Beziehungskomplex von der als Mittelbegriff funktionierenden Größe zu einer der beiden anderen Größen. Von der zweiten anderen Größe wird dann gesagt, daß von ihr wegen jenes Gegensatzes der Beziehungen auch oder erst recht gilt, was vom Mittelbegriff gilt. Bei einer embryonalen Form dieser Operationsweise bestimmt die Auffassung des Gegensatzes der Richtungen nur die Synthesis der Beziehungen zu einem anschaulichen Gesamttatbestand von repräsentativer Bedeutung, worauf dann ein Ablesen erfolgt. Diese Schlußweise habe ich gefunden bei Schlüssen mit räumlichen Beziehungen und mit zeitlichen Beziehungen. Bei Schlüssen mit den Beziehungen "größer - kleiner" ist sie mir nicht entgegengetreten, sie ist aber auch eine mögliche Betrachtungsweise. Dagegen findet sie sich nicht bei Schlüssen mit einer Subsumtionsbeziehung. Wie hier die Geltung allgemeiner Schlüsse für unendlich viele Fälle bedingt ist, ergibt sich nach meinen früheren Entwicklungen von selbst. - Ich hätte nun noch von den beiden dieser vier Operationsweisen, welche sich nicht in der hier besprochenen Form bei Subsumtionsschlüssen finden, das Analoge bei Subsumtionsschlüssen aufzuweisen. Dabei werden wir eine andere Art des Schlusses für unendlich viele Fälle kennen lernen. Wenn mir die Prämissen gegeben sind:
Oder man kann den Schluß ziehen, indem man sich beim Schließen auf den Gedanken der Gleichheit der Beziehung stützt in der von mir an dritter Stelle besprochenen Weise des Operierens. Ich kann den Schluß aber auch auf anderem Weg vollziehen: durch Substitution, Einsetzung; ich kann die erstgedachte Gattung (S) als Teil der zweitgedachten Gattung (R) auffassen und sagen: Was vom Ganzen (R) gilt, das gilt auch von einem Teil derselben (S). Da das Ganze (R) zur Gattung F gehört, so gehört auch ein Teil desselben (S) zur Gattung F. Inwiefern in diesem Verfahren ein Analogon für die zwei oben besprochenen Operationsweisen liegt, brauche ich für unseren Zweck hier nicht auszuführen, ich habe das an einem anderen Ort nachgewiesen (23). Uns interessiert hier, daß wir hier auch eine Bestimmung für unendlich viele Fälle gemacht haben, aber ohne daß wir uns auf die Gleichförmigkeit des Raumgebildes, des Zeitgebildes der Zahlenreihe gestützt haben - oder genauer: eine Bestimmung, die für unendlich viele Fälle gilt, wenn die Prämissen auf unendlich viele Fälle Anwendung finden. (Dieser letztere Unterschied der Gattungsschlüsse im Gegensatz zu den Schlüssen mit räumlichen Beziehungen, zeitlichen Beziehungen und den Beziehungen "größer-kleiner" trat uns ja schon früher hervor.) Wie ist nun hier der Schluß, eventuell für unendlich viele Fälle bedingt? Darauf ist zu sagen: Hier haben wir mögliche Beziehungen von Objekten abstrakt fixiert und diese abstrakten Größen sind wieder in Beziehung zueinander gestellt. Unsere Schluß-Bestimmungen gelten für alles, was die in den Prämissen abstrakt bezeichneten Merkmale an sich trägt. Bei der Besprechung des arithmetischen und geometrischen Denkens werden uns diese beiden Arten des Schließens für unendlich viele Fälle wieder begegnen. Dort werden die hier gemachten Bestimmungen zugleich Ergänzungen erfahren. Hier will ich nur noch hervorheben, daß die hier zu zweit besprochene Art von Schlüssen für unendlich viele Fälle sich auch bei hypothetischen und disjunktiven Schlüssen realisiert findet. Das Hauptresultat, welches wir hier für die Erkenntnistheorie gewonnen haben, ist dieses, daß im schließenden Denken Bestimmungen gemacht werden können, die synthetisch und a priori sind im Gebiet der formalen Wissenschaften außerhalb des Gebiets des arithmetischen Denkens. KANT wirft bekanntlich HUME vor, daß er sich sein Problem nicht allgemein genug vorgestellt hat (24). Mir scheint, daß man KANT denselben Einwand zu machen hat: hätte er diese synthetischen Bestimmungen a priori beachtet, so würde ihn die Lösung der Frage "wie sind synthetische Urteile a priori möglich?" besser gelungen sein. Mit dem Hinweis auf diese Tatbestände vindizieren wir dem Denken selbst eine größere Bedeutung als das bisher geschehen ist. Diese erkenntnistheoretische Position möchte ich kurz im Gegensatz zum dogmatischen Rationalismus, der sich besonders auf die Realitätsprobleme bezieht, als kritischen Rationalismus bezüglich der formalen Wissenschaften ohne die Annahme des Angeborenseins der betreffenden Beziehungsgedanken - kurz ohne die Annahme eines psychologischen a priori - bezeichnen. Dabei hebe ich hier schon hervor, daß ich bei erkenntnistheoretischer Behandlung der Realitätsprobleme von einem rationalistischen Standpunkt sehr weit entfernt bin.
1) Dieser Abschnitt kann auch nach dem 2. Abschnitt über die Realitätsprobleme gelesen werden. 2) Experimentelle und psychopathologische Untersuchungen über das Bewußtsein der Gültigkeit, Archiv für die gesamte Psychologie, Bd. 14, Leipzig 1909. 3) Störring, a. a. O., Archiv für die gesamte Psychologie 4) a. a. O., Seite 15f. 5) Rickert, Gegenstand der Erkenntnis, zweite Auflage 1904, Seite 113. 6) Rickert, a. a. O., Seite 128 7) Rickert, a. a. O., Seite 129-132. 8) Plato, Theatet, Kapitel XIV, Schluß; vgl. Laas, Idealismus und Positivismus, Bd. 1, Seite 39f. 9) Sextus Empiricus, Grundzüge der pyrrhonischen Skepsis, Seite 28 und 29. 10) Descartes, Meditationen (Philosophisches Bibliothek, hg. Kirchmann), Seite 22f. 11) Descartes, Abhandlung über die Methode (Kirchmann) Seite 46. 12) Herbart, Allgemeine Metaphysik (Ausgabe Kehrbach) Seite 53. 13) Sigwart, Logik I, Seite 460f; Wundt, Logik I, Seite 319f. 14) Experimentelle Untersuchungen über einfache Schlußprozesse, Archiv für die gesamte Psychologie, Bd. 11, Seite 13. 15) a. a. O., Seite 5f 16) a. a. O., Seite 34f 17) a. a. O., Seite 54f 18) a. a. O., Seite 77f 19) a. a. O., Seite Seite 20f 20) a. a. O., Seite 61f 21) a. a. O., Seite 99. 22) a. a. O., Seite 100f 23) a. a. O., Seite 99. 24) Kant, Prolegomena (Ausgabe Erdmann) Seite 21. |